Arbitrary non-Correlated Symbols
Notations:
When summation interval is obvious, we'll omit limits at summ sign:
 j can mean
j can mean  j=0,n-1
Definitions:
L = Maximum number of chips in symbol.
Tc = Duration of one chip.
C=Tc*L. C = Maximum possible duration of one symbol.
Signal (message) x=
j=0,n-1
Definitions:
L = Maximum number of chips in symbol.
Tc = Duration of one chip.
C=Tc*L. C = Maximum possible duration of one symbol.
Signal (message) x=  j=0,n-1 xj (1)
where:
xj(t)=Saj(t-cj) (j)
- is a signal of symbol aj started (centered) at time cj
j - (time) index of symbol in a message,
aj is in Alphabet of symbols.
Alphabet={0,1,...N-1}.
For example N=2M for OOK.
M = number of bits comprising each symbol.
Sb(t) - "waveform,shape" of a symbol b.
Note:
Sb is not neccesary a step function or reachtngular pulse.
Rectangular pulse, Sb(t) = Abp(t-tb) {P}
will be consider later.
Signals Sb do not necessary have the same time length L.
For example, for DAPPM sequences 01 and 002.
Hence, we don't assume that cj=Tc*L*j yet.
In (1), a is a random function aj of index j.
In article [1], k denotes index such kTc=ta+jC for equilength symbol messages.
Our first goal is to reseach spectrum of power.
Autocorrelation function is R(tau)= E[x(0)x(0-tau)]/I. (R)
I - average power, I=E[x2(0)].
We are not interested in research of specific sequences of symbols. We are reseaching properties of
communication channel. So, for our convenience, we take a sequence of uniformly distributed non-correlated symbols.
Intuitively, because of set of symbols is finite, there exists enough big T such the interval [0,T] will be sufficient sample
to bear atocorrelation properties for tau << T.
For our convenience, we extend function x(t) periodically below 0 and beyond T. x is defined on all |R-axis.
We are ready to calculate expectation in following form:
R(tau)=1/TI
j=0,n-1 xj (1)
where:
xj(t)=Saj(t-cj) (j)
- is a signal of symbol aj started (centered) at time cj
j - (time) index of symbol in a message,
aj is in Alphabet of symbols.
Alphabet={0,1,...N-1}.
For example N=2M for OOK.
M = number of bits comprising each symbol.
Sb(t) - "waveform,shape" of a symbol b.
Note:
Sb is not neccesary a step function or reachtngular pulse.
Rectangular pulse, Sb(t) = Abp(t-tb) {P}
will be consider later.
Signals Sb do not necessary have the same time length L.
For example, for DAPPM sequences 01 and 002.
Hence, we don't assume that cj=Tc*L*j yet.
In (1), a is a random function aj of index j.
In article [1], k denotes index such kTc=ta+jC for equilength symbol messages.
Our first goal is to reseach spectrum of power.
Autocorrelation function is R(tau)= E[x(0)x(0-tau)]/I. (R)
I - average power, I=E[x2(0)].
We are not interested in research of specific sequences of symbols. We are reseaching properties of
communication channel. So, for our convenience, we take a sequence of uniformly distributed non-correlated symbols.
Intuitively, because of set of symbols is finite, there exists enough big T such the interval [0,T] will be sufficient sample
to bear atocorrelation properties for tau << T.
For our convenience, we extend function x(t) periodically below 0 and beyond T. x is defined on all |R-axis.
We are ready to calculate expectation in following form:
R(tau)=1/TI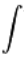 0,T x(t)x(t-tau)dt (R')
Now it is time to involve Fourier transformation.
Because of x has period T, Rw=|xw|2, (R'')
where circular frequncy w=2 PI f = 2 PI m/ T,
x=
0,T x(t)x(t-tau)dt (R')
Now it is time to involve Fourier transformation.
Because of x has period T, Rw=|xw|2, (R'')
where circular frequncy w=2 PI f = 2 PI m/ T,
x= m=-oo,oo xweiwt. (F)
Like original signal x, its Fourier transform will be a summ of sinals via nodes j:
xw=
m=-oo,oo xweiwt. (F)
Like original signal x, its Fourier transform will be a summ of sinals via nodes j:
xw= j xw,j.
We need to find a way to exlcude "randomness" brought by random function Ss.
We will take average:
<Rw>=<xwxw*>
This is an artificial step, because Rw is already averaged:
Rw=<Rw>
but this step make our derivations easy.
We have:
Rw=(1/I)
j xw,j.
We need to find a way to exlcude "randomness" brought by random function Ss.
We will take average:
<Rw>=<xwxw*>
This is an artificial step, because Rw is already averaged:
Rw=<Rw>
but this step make our derivations easy.
We have:
Rw=(1/I) jj' <xwjx*wj'>
Constant length symbols
Consider messages where each symbol takes equal number of chips L.
Because symbols follow independently:
<xwjx*wj'> =
<xwj><x*wj'> for j=/=j', (N)
<xwjx*wj>=D for j=j'. (D)
Expanding (j), we reduce average for S to average W via alphabet:
<xwj> = <Swj> = e-iwjC W.
W=(1/N)
jj' <xwjx*wj'>
Constant length symbols
Consider messages where each symbol takes equal number of chips L.
Because symbols follow independently:
<xwjx*wj'> =
<xwj><x*wj'> for j=/=j', (N)
<xwjx*wj>=D for j=j'. (D)
Expanding (j), we reduce average for S to average W via alphabet:
<xwj> = <Swj> = e-iwjC W.
W=(1/N)  a=1,N Saw.
Average for j=j' does not contain message structure factor and is merely in form SS*:
D=<xwjx*wj> =(1/N)
a=1,N Saw.
Average for j=j' does not contain message structure factor and is merely in form SS*:
D=<xwjx*wj> =(1/N) bSbS*b.
Our expression for R takes a form:
Rw=(1/I)( Jw W'w + nDw),
where:
W'w=WwWw*,
and factor:
Jw =
bSbS*b.
Our expression for R takes a form:
Rw=(1/I)( Jw W'w + nDw),
where:
W'w=WwWw*,
and factor:
Jw =  j=/=j' e-iwC(j-j') =
-n +
j=/=j' e-iwC(j-j') =
-n +  jj' e-iwC(j-j') =
-n + FF*,
where:
F=
jj' e-iwC(j-j') =
-n + FF*,
where:
F= j e-iwCj=
(using geometric-progression formula)
=(1-e-iwCn)(1-e-iwC)=0 because of
Cn=T and wCn=2 PI m.
However, F=0 is correct for w=/=0.
Expanding exponents till first order in wCn, we have:
(1-(1-iwCn))/(1-(1-iwC))=n. Because of F is continuous in 0,
Fw|w=0=n.
The only interest we have in knowing values at w=0 is to
see that final formulas for R will have correct average = <R>.
In other words, Fw=n dw,0, where
d is Kroneckers delta.
Finally, for constant length symbols:
Rw=n/I(D-(1-ndw,0)W');
We will often omit delta-member wich still will be correct for w=/=0:
Rw=n/I(D-W');
Now, let us to consider rectangular bar pulse {P}:
Sbw = Abwpwe-iwdbTc
d is an offset of a pulse for symbol b relatively to t=0.
pw=(1/T)
j e-iwCj=
(using geometric-progression formula)
=(1-e-iwCn)(1-e-iwC)=0 because of
Cn=T and wCn=2 PI m.
However, F=0 is correct for w=/=0.
Expanding exponents till first order in wCn, we have:
(1-(1-iwCn))/(1-(1-iwC))=n. Because of F is continuous in 0,
Fw|w=0=n.
The only interest we have in knowing values at w=0 is to
see that final formulas for R will have correct average = <R>.
In other words, Fw=n dw,0, where
d is Kroneckers delta.
Finally, for constant length symbols:
Rw=n/I(D-(1-ndw,0)W');
We will often omit delta-member wich still will be correct for w=/=0:
Rw=n/I(D-W');
Now, let us to consider rectangular bar pulse {P}:
Sbw = Abwpwe-iwdbTc
d is an offset of a pulse for symbol b relatively to t=0.
pw=(1/T)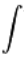 0,Tc e-iwtdt=
=(1-e-iwG)/(iwT) = e-iwG/2 (2i sin(iwG/2))/(iwGnL) =
= e-iwG/2/nL sin((pi)g)/((pi)g) =
= e-iwG/2/nL sinc(g)
G=Tc
f=m/T - frequency
g=fG - unitless parameter
q=wG/2 = 2(pi)m/TG/2 = (pi)g
We need only Pw = |pw|2 = 1/(nnLL) sinc2(g)
For OOK, PPM, DAPPM(when neglecting effect of symbol offset shift?):
D = 1/(nnLL)PQ.
W' = 1/(nnLL)PKH.
Q=1/N
0,Tc e-iwtdt=
=(1-e-iwG)/(iwT) = e-iwG/2 (2i sin(iwG/2))/(iwGnL) =
= e-iwG/2/nL sin((pi)g)/((pi)g) =
= e-iwG/2/nL sinc(g)
G=Tc
f=m/T - frequency
g=fG - unitless parameter
q=wG/2 = 2(pi)m/TG/2 = (pi)g
We need only Pw = |pw|2 = 1/(nnLL) sinc2(g)
For OOK, PPM, DAPPM(when neglecting effect of symbol offset shift?):
D = 1/(nnLL)PQ.
W' = 1/(nnLL)PKH.
Q=1/N  bAb2
K=1/(NN) (
bAb2
K=1/(NN) ( s=1,A As)2
H=
s=1,A As)2
H=  dd'=0,L-1 eiw(d-d')G.
R=1/(nLLNI) P(Q-KH)
For OOK,
For OOK, we considered Alphabet as having 2 symbols and each chip will carry exactly one symbol 0 or 1:
C=G. N=2. L=1. A=1. I=1/2.
Q = 1/2
K = 1/4
H = 1
R = 1/n P(1/2-KH) = 1/(4n) P
To see R0, we replace KH with delta-member, -n/4 and obtain R0=1/4.
Does reader think this is correct?
Without normalizing by I, R=1/(8n) P. What if to take P/8 as a reference?
For PPM:
N = L
Q = (1+1+....+1)/N=1
K = 1/N
H =
dd'=0,L-1 eiw(d-d')G.
R=1/(nLLNI) P(Q-KH)
For OOK,
For OOK, we considered Alphabet as having 2 symbols and each chip will carry exactly one symbol 0 or 1:
C=G. N=2. L=1. A=1. I=1/2.
Q = 1/2
K = 1/4
H = 1
R = 1/n P(1/2-KH) = 1/(4n) P
To see R0, we replace KH with delta-member, -n/4 and obtain R0=1/4.
Does reader think this is correct?
Without normalizing by I, R=1/(8n) P. What if to take P/8 as a reference?
For PPM:
N = L
Q = (1+1+....+1)/N=1
K = 1/N
H =  dd'=0,L-1 cos(2(pi)g(d-d') =
L + 2
dd'=0,L-1 cos(2(pi)g(d-d') =
L + 2 d=1,L-1 (L-d)cos(2(pi)gd)
I = 1/L
R = 1/(nLL) P (1-KH)
To see R0, we replace KH with delta-member, -nKH=-nL and obtain R0=1/L.
Does reader think this is correct?
To make I=A2/L the same levlel as for OOK, 1/2, we need to increase amplitude in sqrt(L/2) times which
increases non-normalized R by L/2 which gives 1/(nLL2) P(...).
We have to compare OOK with 1/(2LL) P(1-KH), or P against 4/(LL).
Coding Scheme Properties
Unit of measure denoted in [...].
(Really strange definition:)
Transimission Capacity = (Number of Bits in full alphabet)/(Average number of chips in symbol). [Bit/Chip].
DAPPM: M *(Number of symbols) / ((L+1)/2) = 2MAL/(L+1). [1(8)]
= 2MA2M/(2M+A) [1Tabl.2]
PPM: M * 2M / 2M = M
d=1,L-1 (L-d)cos(2(pi)gd)
I = 1/L
R = 1/(nLL) P (1-KH)
To see R0, we replace KH with delta-member, -nKH=-nL and obtain R0=1/L.
Does reader think this is correct?
To make I=A2/L the same levlel as for OOK, 1/2, we need to increase amplitude in sqrt(L/2) times which
increases non-normalized R by L/2 which gives 1/(nLL2) P(...).
We have to compare OOK with 1/(2LL) P(1-KH), or P against 4/(LL).
Coding Scheme Properties
Unit of measure denoted in [...].
(Really strange definition:)
Transimission Capacity = (Number of Bits in full alphabet)/(Average number of chips in symbol). [Bit/Chip].
DAPPM: M *(Number of symbols) / ((L+1)/2) = 2MAL/(L+1). [1(8)]
= 2MA2M/(2M+A) [1Tabl.2]
PPM: M * 2M / 2M = M

 j can mean
j can mean  j=0,n-1
Definitions:
L = Maximum number of chips in symbol.
Tc = Duration of one chip.
C=Tc*L. C = Maximum possible duration of one symbol.
Signal (message) x=
j=0,n-1
Definitions:
L = Maximum number of chips in symbol.
Tc = Duration of one chip.
C=Tc*L. C = Maximum possible duration of one symbol.
Signal (message) x=  j=0,n-1 xj (1)
where:
xj(t)=Saj(t-cj) (j)
- is a signal of symbol aj started (centered) at time cj
j - (time) index of symbol in a message,
aj is in Alphabet of symbols.
Alphabet={0,1,...N-1}.
For example N=2M for OOK.
M = number of bits comprising each symbol.
Sb(t) - "waveform,shape" of a symbol b.
Note:
Sb is not neccesary a step function or reachtngular pulse.
Rectangular pulse, Sb(t) = Abp(t-tb) {P}
will be consider later.
Signals Sb do not necessary have the same time length L.
For example, for DAPPM sequences 01 and 002.
Hence, we don't assume that cj=Tc*L*j yet.
In (1), a is a random function aj of index j.
In article [1], k denotes index such kTc=ta+jC for equilength symbol messages.
Our first goal is to reseach spectrum of power.
Autocorrelation function is R(tau)= E[x(0)x(0-tau)]/I. (R)
I - average power, I=E[x2(0)].
We are not interested in research of specific sequences of symbols. We are reseaching properties of
communication channel. So, for our convenience, we take a sequence of uniformly distributed non-correlated symbols.
Intuitively, because of set of symbols is finite, there exists enough big T such the interval [0,T] will be sufficient sample
to bear atocorrelation properties for tau << T.
For our convenience, we extend function x(t) periodically below 0 and beyond T. x is defined on all |R-axis.
We are ready to calculate expectation in following form:
R(tau)=1/TI
j=0,n-1 xj (1)
where:
xj(t)=Saj(t-cj) (j)
- is a signal of symbol aj started (centered) at time cj
j - (time) index of symbol in a message,
aj is in Alphabet of symbols.
Alphabet={0,1,...N-1}.
For example N=2M for OOK.
M = number of bits comprising each symbol.
Sb(t) - "waveform,shape" of a symbol b.
Note:
Sb is not neccesary a step function or reachtngular pulse.
Rectangular pulse, Sb(t) = Abp(t-tb) {P}
will be consider later.
Signals Sb do not necessary have the same time length L.
For example, for DAPPM sequences 01 and 002.
Hence, we don't assume that cj=Tc*L*j yet.
In (1), a is a random function aj of index j.
In article [1], k denotes index such kTc=ta+jC for equilength symbol messages.
Our first goal is to reseach spectrum of power.
Autocorrelation function is R(tau)= E[x(0)x(0-tau)]/I. (R)
I - average power, I=E[x2(0)].
We are not interested in research of specific sequences of symbols. We are reseaching properties of
communication channel. So, for our convenience, we take a sequence of uniformly distributed non-correlated symbols.
Intuitively, because of set of symbols is finite, there exists enough big T such the interval [0,T] will be sufficient sample
to bear atocorrelation properties for tau << T.
For our convenience, we extend function x(t) periodically below 0 and beyond T. x is defined on all |R-axis.
We are ready to calculate expectation in following form:
R(tau)=1/TI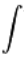 0,T x(t)x(t-tau)dt (R')
Now it is time to involve Fourier transformation.
Because of x has period T, Rw=|xw|2, (R'')
where circular frequncy w=2 PI f = 2 PI m/ T,
x=
0,T x(t)x(t-tau)dt (R')
Now it is time to involve Fourier transformation.
Because of x has period T, Rw=|xw|2, (R'')
where circular frequncy w=2 PI f = 2 PI m/ T,
x= m=-oo,oo xweiwt. (F)
Like original signal x, its Fourier transform will be a summ of sinals via nodes j:
xw=
m=-oo,oo xweiwt. (F)
Like original signal x, its Fourier transform will be a summ of sinals via nodes j:
xw= j xw,j.
We need to find a way to exlcude "randomness" brought by random function Ss.
We will take average:
<Rw>=<xwxw*>
This is an artificial step, because Rw is already averaged:
Rw=<Rw>
but this step make our derivations easy.
We have:
Rw=(1/I)
j xw,j.
We need to find a way to exlcude "randomness" brought by random function Ss.
We will take average:
<Rw>=<xwxw*>
This is an artificial step, because Rw is already averaged:
Rw=<Rw>
but this step make our derivations easy.
We have:
Rw=(1/I) jj' <xwjx*wj'>
Constant length symbols
Consider messages where each symbol takes equal number of chips L.
Because symbols follow independently:
<xwjx*wj'> =
<xwj><x*wj'> for j=/=j', (N)
<xwjx*wj>=D for j=j'. (D)
Expanding (j), we reduce average for S to average W via alphabet:
<xwj> = <Swj> = e-iwjC W.
W=(1/N)
jj' <xwjx*wj'>
Constant length symbols
Consider messages where each symbol takes equal number of chips L.
Because symbols follow independently:
<xwjx*wj'> =
<xwj><x*wj'> for j=/=j', (N)
<xwjx*wj>=D for j=j'. (D)
Expanding (j), we reduce average for S to average W via alphabet:
<xwj> = <Swj> = e-iwjC W.
W=(1/N)  a=1,N Saw.
Average for j=j' does not contain message structure factor and is merely in form SS*:
D=<xwjx*wj> =(1/N)
a=1,N Saw.
Average for j=j' does not contain message structure factor and is merely in form SS*:
D=<xwjx*wj> =(1/N) bSbS*b.
Our expression for R takes a form:
Rw=(1/I)( Jw W'w + nDw),
where:
W'w=WwWw*,
and factor:
Jw =
bSbS*b.
Our expression for R takes a form:
Rw=(1/I)( Jw W'w + nDw),
where:
W'w=WwWw*,
and factor:
Jw =  j=/=j' e-iwC(j-j') =
-n +
j=/=j' e-iwC(j-j') =
-n +  jj' e-iwC(j-j') =
-n + FF*,
where:
F=
jj' e-iwC(j-j') =
-n + FF*,
where:
F= j e-iwCj=
(using geometric-progression formula)
=(1-e-iwCn)(1-e-iwC)=0 because of
Cn=T and wCn=2 PI m.
However, F=0 is correct for w=/=0.
Expanding exponents till first order in wCn, we have:
(1-(1-iwCn))/(1-(1-iwC))=n. Because of F is continuous in 0,
Fw|w=0=n.
The only interest we have in knowing values at w=0 is to
see that final formulas for R will have correct average = <R>.
In other words, Fw=n dw,0, where
d is Kroneckers delta.
Finally, for constant length symbols:
Rw=n/I(D-(1-ndw,0)W');
We will often omit delta-member wich still will be correct for w=/=0:
Rw=n/I(D-W');
Now, let us to consider rectangular bar pulse {P}:
Sbw = Abwpwe-iwdbTc
d is an offset of a pulse for symbol b relatively to t=0.
pw=(1/T)
j e-iwCj=
(using geometric-progression formula)
=(1-e-iwCn)(1-e-iwC)=0 because of
Cn=T and wCn=2 PI m.
However, F=0 is correct for w=/=0.
Expanding exponents till first order in wCn, we have:
(1-(1-iwCn))/(1-(1-iwC))=n. Because of F is continuous in 0,
Fw|w=0=n.
The only interest we have in knowing values at w=0 is to
see that final formulas for R will have correct average = <R>.
In other words, Fw=n dw,0, where
d is Kroneckers delta.
Finally, for constant length symbols:
Rw=n/I(D-(1-ndw,0)W');
We will often omit delta-member wich still will be correct for w=/=0:
Rw=n/I(D-W');
Now, let us to consider rectangular bar pulse {P}:
Sbw = Abwpwe-iwdbTc
d is an offset of a pulse for symbol b relatively to t=0.
pw=(1/T)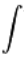 0,Tc e-iwtdt=
=(1-e-iwG)/(iwT) = e-iwG/2 (2i sin(iwG/2))/(iwGnL) =
= e-iwG/2/nL sin((pi)g)/((pi)g) =
= e-iwG/2/nL sinc(g)
G=Tc
f=m/T - frequency
g=fG - unitless parameter
q=wG/2 = 2(pi)m/TG/2 = (pi)g
We need only Pw = |pw|2 = 1/(nnLL) sinc2(g)
For OOK, PPM, DAPPM(when neglecting effect of symbol offset shift?):
D = 1/(nnLL)PQ.
W' = 1/(nnLL)PKH.
Q=1/N
0,Tc e-iwtdt=
=(1-e-iwG)/(iwT) = e-iwG/2 (2i sin(iwG/2))/(iwGnL) =
= e-iwG/2/nL sin((pi)g)/((pi)g) =
= e-iwG/2/nL sinc(g)
G=Tc
f=m/T - frequency
g=fG - unitless parameter
q=wG/2 = 2(pi)m/TG/2 = (pi)g
We need only Pw = |pw|2 = 1/(nnLL) sinc2(g)
For OOK, PPM, DAPPM(when neglecting effect of symbol offset shift?):
D = 1/(nnLL)PQ.
W' = 1/(nnLL)PKH.
Q=1/N  bAb2
K=1/(NN) (
bAb2
K=1/(NN) ( s=1,A As)2
H=
s=1,A As)2
H=  dd'=0,L-1 eiw(d-d')G.
R=1/(nLLNI) P(Q-KH)
For OOK,
For OOK, we considered Alphabet as having 2 symbols and each chip will carry exactly one symbol 0 or 1:
C=G. N=2. L=1. A=1. I=1/2.
Q = 1/2
K = 1/4
H = 1
R = 1/n P(1/2-KH) = 1/(4n) P
To see R0, we replace KH with delta-member, -n/4 and obtain R0=1/4.
Does reader think this is correct?
Without normalizing by I, R=1/(8n) P. What if to take P/8 as a reference?
For PPM:
N = L
Q = (1+1+....+1)/N=1
K = 1/N
H =
dd'=0,L-1 eiw(d-d')G.
R=1/(nLLNI) P(Q-KH)
For OOK,
For OOK, we considered Alphabet as having 2 symbols and each chip will carry exactly one symbol 0 or 1:
C=G. N=2. L=1. A=1. I=1/2.
Q = 1/2
K = 1/4
H = 1
R = 1/n P(1/2-KH) = 1/(4n) P
To see R0, we replace KH with delta-member, -n/4 and obtain R0=1/4.
Does reader think this is correct?
Without normalizing by I, R=1/(8n) P. What if to take P/8 as a reference?
For PPM:
N = L
Q = (1+1+....+1)/N=1
K = 1/N
H =  dd'=0,L-1 cos(2(pi)g(d-d') =
L + 2
dd'=0,L-1 cos(2(pi)g(d-d') =
L + 2 d=1,L-1 (L-d)cos(2(pi)gd)
I = 1/L
R = 1/(nLL) P (1-KH)
To see R0, we replace KH with delta-member, -nKH=-nL and obtain R0=1/L.
Does reader think this is correct?
To make I=A2/L the same levlel as for OOK, 1/2, we need to increase amplitude in sqrt(L/2) times which
increases non-normalized R by L/2 which gives 1/(nLL2) P(...).
We have to compare OOK with 1/(2LL) P(1-KH), or P against 4/(LL).
Coding Scheme Properties
Unit of measure denoted in [...].
(Really strange definition:)
Transimission Capacity = (Number of Bits in full alphabet)/(Average number of chips in symbol). [Bit/Chip].
DAPPM: M *(Number of symbols) / ((L+1)/2) = 2MAL/(L+1). [1(8)]
= 2MA2M/(2M+A) [1Tabl.2]
PPM: M * 2M / 2M = M
d=1,L-1 (L-d)cos(2(pi)gd)
I = 1/L
R = 1/(nLL) P (1-KH)
To see R0, we replace KH with delta-member, -nKH=-nL and obtain R0=1/L.
Does reader think this is correct?
To make I=A2/L the same levlel as for OOK, 1/2, we need to increase amplitude in sqrt(L/2) times which
increases non-normalized R by L/2 which gives 1/(nLL2) P(...).
We have to compare OOK with 1/(2LL) P(1-KH), or P against 4/(LL).
Coding Scheme Properties
Unit of measure denoted in [...].
(Really strange definition:)
Transimission Capacity = (Number of Bits in full alphabet)/(Average number of chips in symbol). [Bit/Chip].
DAPPM: M *(Number of symbols) / ((L+1)/2) = 2MAL/(L+1). [1(8)]
= 2MA2M/(2M+A) [1Tabl.2]
PPM: M * 2M / 2M = M
