F l a t m o t i o n o f a p a r t i c l e.
Consider a particle with mass m, radius-vector r, and velocity v=rt.
The force applied to particle belongs the plane v,rtt. If in following moments this force
still does not change this plane, then the trajectory of the particle will
belong this plane. In following examples, we consider such forces.
Plane motion has 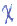 =0 in FS-formulas.
Vectors r,v describe the motion of our particle in some approximately inertial system
which we will call "Local System" (LS). "Approximately" means that the Local System is
inertial with degree of accuracy acceptable by us. For example, for projectile
motion, we take Earth's surface as a "Local System" because Earth's movement
to common center of mass of Earth and our particle is neglectful, and both
Local System and Center of mass system can be "inertial".
Following is a draft:
A. C i r c u l a r m o t i o n.
This motion is equivalent to condition: |r|=R
=> rr=const <=>
rrt=0. (n)
Circular motion can be compactly described in complex notations:
r=Re(ib), b is an angle.
velocity =rt=iRe(ib)bt=btir=uRbt which confirms ortogonality (n) again.
acceleration=rtt=-rbt2 + uRbtt ('')
which is a summ of normal and tangent components correspondingly.
The latter result also follows from FS notations:
rt=rsst=usbbt=uRbt=k'*rbt
rtt=k'*uRbt2+uRbtt
k' is normal to u and r.
k'=k. => k*u=-r=nR, and
rtt=nRbt2+uRbtt
Letting variable t=s, we see bt=1/R, and curvature vector rss=nRbs2=n/R.
Therefore curvature c=1/R.
usR2bt2+uRbtt=ncR2bt2+uRbtt
At the moment, we don't see the path simpler than use formula for curvature c:
c=bs3R2=1/R.
Following is a draft:
We need vector notation for angular speed, w, which in our case simplifies to
w=r*v/RR, *-vector product.
=> v=w*r.
We will use normal to plane of motion, vector n=w0/|w0|, taken at t=0.
Then w=Wn, where W=B', is a real number which changes the sign when angle motion
changes orientation.
In complex notations: r' = irW
r''=-rWW + irW'
System O. B o d y i n C i r c u l a r M o t i o n.
Consider the system: body + rod + pin + planet.
Consider that we
1) neglect gravitation of the Planet,
2) no other forces act on body except from the rod, no air friction.
3) body size is small comparing other parameters of our system, so we
consider this body as a particle.
4) we assume that force from the rod to a body is always acts along
the line of the rod. It is obvious, but perhaps difficult to prove
when to go deeply to details with specific systems.
5) mass of the planet is much greater than mass of the body.
4) => irW''=0. Only normal acceleration exists.
=>
Full mathematical description of Equation of Motions of the particle is (EMI):
Force f=mr''=-mWWr (i)
r(0)=r0 - initial position (ii)
v(0)=v0 - initial speed (iii)
r=e(iA)R (e)
Note, that numbers F0=-mW0W0R and v0=W0R constrain each other:
v0 and R constrain W0, which constrains F0.
Otherwise, force's absolute value, F, can have any dependence from t, F(t);
however, we consider further the following system:
System I. B o d y i n U n i f o r m ? C i r c u l a r M o t i o n.
6) F=const. It is perhaps obvious that such systems exist, but difficult
to prove in each specific case.
Now, it is easy to write down a solution for above system of differential
equations (EMI):
it is simply W=const=V/R
We will use special notation for this value P (Phase speed).
This solution is unique, which should follow from corresponding mathematical
theorem which is out of scope of this intro.
For choice of initial conditions:
r0=(0,-R) (For better analogy with spring)
v0=(V,0)
the solution is:
x=Rsin(Pt)
y=-Rcos(Pt)
P=W=V/R
F=mPPR
We can add that cinetic energy is T=mVV/2=const and has two components:
for motion along each direction T=m(VxVx)/2 + m(VyVy)/2.
System II. S p r i n g. A n a l o g y w i t h S y s t e m I.
fx=-kx=Mx''
x0=0
x'(0)=V
Solution:
System (EMI) equivalent to two systems for each direction, and we
will write just for x direction:
fx=-mPPx=mx'' (*')
x(0)=0 - initial position (1')
x'(0)=V - initial speed (2')
Therefore, system for spring and x-coordinate of rotating particle are
equivalent and have the same solution if to take:
P=sqrt(k/M)
This analogy extends to following values:
Left part - circular motion, right part - spring:
Vx=x'
Ax=Vx'
m =M
Tx=T or m(VxVx)/2 = MVxVx/2
Ty=U or m(VyVy)/2 = kxx/2
E =E full energy.
System III. M a t h e m a t i c a l P e n d u l u m.
This is a System O where not only force from rod applied, but
also a gravitation force mg.
Equation of motion will look:
x''=-gsin(B)cos(B)
x0=0,
x'(0)=V.
y is bound by rod to x, we don't worry about it now:
xx+yy=RR
We assume that "rod is passive and react in such way that"
summ of forces along the rod's line is 0.
We restrict ourselves by considering the case when initial
speed V is so small that amplitude of angle B is so small that
we can use Taylor's expansion for sin and cos:
sin(B)=~B
cos(B)=~1-BB/2
To derive the condition for such approximation we equate:
mgh=mVV/2 or gh=VV/2.
h<<R <=> VV/(2g)<<R <=> WW<<g/R
x''=-gB=-(g/R)x
x0=0,
x'(0)=V.
Now, we again using solution (EMI) by taking P=sqrt(g/R):
W=Qsin(Pt), Q=W0.
We need to calculate the amplitude Q:
VV/2=QQRg. Q=sqrt(VV/(2Rg)).
W'0=QPcos(0)=V/R => QP=V/R => Q=sqrt(R/gVV/RR)=sqrt(VV/g/R)
x=Xsin(Pt), X=QR.
Vx=QRPcos(Pt).
Cinetic energy, T=mVV/2 cos(p)cos(p)
Potential energy, U=mgh=mgXW=mgsin(p)sin(p)RQQ=mVV/2 sin(p)sin(p)
We see: T+U=E.
=0 in FS-formulas.
Vectors r,v describe the motion of our particle in some approximately inertial system
which we will call "Local System" (LS). "Approximately" means that the Local System is
inertial with degree of accuracy acceptable by us. For example, for projectile
motion, we take Earth's surface as a "Local System" because Earth's movement
to common center of mass of Earth and our particle is neglectful, and both
Local System and Center of mass system can be "inertial".
Following is a draft:
A. C i r c u l a r m o t i o n.
This motion is equivalent to condition: |r|=R
=> rr=const <=>
rrt=0. (n)
Circular motion can be compactly described in complex notations:
r=Re(ib), b is an angle.
velocity =rt=iRe(ib)bt=btir=uRbt which confirms ortogonality (n) again.
acceleration=rtt=-rbt2 + uRbtt ('')
which is a summ of normal and tangent components correspondingly.
The latter result also follows from FS notations:
rt=rsst=usbbt=uRbt=k'*rbt
rtt=k'*uRbt2+uRbtt
k' is normal to u and r.
k'=k. => k*u=-r=nR, and
rtt=nRbt2+uRbtt
Letting variable t=s, we see bt=1/R, and curvature vector rss=nRbs2=n/R.
Therefore curvature c=1/R.
usR2bt2+uRbtt=ncR2bt2+uRbtt
At the moment, we don't see the path simpler than use formula for curvature c:
c=bs3R2=1/R.
Following is a draft:
We need vector notation for angular speed, w, which in our case simplifies to
w=r*v/RR, *-vector product.
=> v=w*r.
We will use normal to plane of motion, vector n=w0/|w0|, taken at t=0.
Then w=Wn, where W=B', is a real number which changes the sign when angle motion
changes orientation.
In complex notations: r' = irW
r''=-rWW + irW'
System O. B o d y i n C i r c u l a r M o t i o n.
Consider the system: body + rod + pin + planet.
Consider that we
1) neglect gravitation of the Planet,
2) no other forces act on body except from the rod, no air friction.
3) body size is small comparing other parameters of our system, so we
consider this body as a particle.
4) we assume that force from the rod to a body is always acts along
the line of the rod. It is obvious, but perhaps difficult to prove
when to go deeply to details with specific systems.
5) mass of the planet is much greater than mass of the body.
4) => irW''=0. Only normal acceleration exists.
=>
Full mathematical description of Equation of Motions of the particle is (EMI):
Force f=mr''=-mWWr (i)
r(0)=r0 - initial position (ii)
v(0)=v0 - initial speed (iii)
r=e(iA)R (e)
Note, that numbers F0=-mW0W0R and v0=W0R constrain each other:
v0 and R constrain W0, which constrains F0.
Otherwise, force's absolute value, F, can have any dependence from t, F(t);
however, we consider further the following system:
System I. B o d y i n U n i f o r m ? C i r c u l a r M o t i o n.
6) F=const. It is perhaps obvious that such systems exist, but difficult
to prove in each specific case.
Now, it is easy to write down a solution for above system of differential
equations (EMI):
it is simply W=const=V/R
We will use special notation for this value P (Phase speed).
This solution is unique, which should follow from corresponding mathematical
theorem which is out of scope of this intro.
For choice of initial conditions:
r0=(0,-R) (For better analogy with spring)
v0=(V,0)
the solution is:
x=Rsin(Pt)
y=-Rcos(Pt)
P=W=V/R
F=mPPR
We can add that cinetic energy is T=mVV/2=const and has two components:
for motion along each direction T=m(VxVx)/2 + m(VyVy)/2.
System II. S p r i n g. A n a l o g y w i t h S y s t e m I.
fx=-kx=Mx''
x0=0
x'(0)=V
Solution:
System (EMI) equivalent to two systems for each direction, and we
will write just for x direction:
fx=-mPPx=mx'' (*')
x(0)=0 - initial position (1')
x'(0)=V - initial speed (2')
Therefore, system for spring and x-coordinate of rotating particle are
equivalent and have the same solution if to take:
P=sqrt(k/M)
This analogy extends to following values:
Left part - circular motion, right part - spring:
Vx=x'
Ax=Vx'
m =M
Tx=T or m(VxVx)/2 = MVxVx/2
Ty=U or m(VyVy)/2 = kxx/2
E =E full energy.
System III. M a t h e m a t i c a l P e n d u l u m.
This is a System O where not only force from rod applied, but
also a gravitation force mg.
Equation of motion will look:
x''=-gsin(B)cos(B)
x0=0,
x'(0)=V.
y is bound by rod to x, we don't worry about it now:
xx+yy=RR
We assume that "rod is passive and react in such way that"
summ of forces along the rod's line is 0.
We restrict ourselves by considering the case when initial
speed V is so small that amplitude of angle B is so small that
we can use Taylor's expansion for sin and cos:
sin(B)=~B
cos(B)=~1-BB/2
To derive the condition for such approximation we equate:
mgh=mVV/2 or gh=VV/2.
h<<R <=> VV/(2g)<<R <=> WW<<g/R
x''=-gB=-(g/R)x
x0=0,
x'(0)=V.
Now, we again using solution (EMI) by taking P=sqrt(g/R):
W=Qsin(Pt), Q=W0.
We need to calculate the amplitude Q:
VV/2=QQRg. Q=sqrt(VV/(2Rg)).
W'0=QPcos(0)=V/R => QP=V/R => Q=sqrt(R/gVV/RR)=sqrt(VV/g/R)
x=Xsin(Pt), X=QR.
Vx=QRPcos(Pt).
Cinetic energy, T=mVV/2 cos(p)cos(p)
Potential energy, U=mgh=mgXW=mgsin(p)sin(p)RQQ=mVV/2 sin(p)sin(p)
We see: T+U=E.
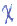 =0 in FS-formulas.
Vectors r,v describe the motion of our particle in some approximately inertial system
which we will call "Local System" (LS). "Approximately" means that the Local System is
inertial with degree of accuracy acceptable by us. For example, for projectile
motion, we take Earth's surface as a "Local System" because Earth's movement
to common center of mass of Earth and our particle is neglectful, and both
Local System and Center of mass system can be "inertial".
Following is a draft:
A. C i r c u l a r m o t i o n.
This motion is equivalent to condition: |r|=R
=> rr=const <=>
rrt=0. (n)
Circular motion can be compactly described in complex notations:
r=Re(ib), b is an angle.
velocity =rt=iRe(ib)bt=btir=uRbt which confirms ortogonality (n) again.
acceleration=rtt=-rbt2 + uRbtt ('')
which is a summ of normal and tangent components correspondingly.
The latter result also follows from FS notations:
rt=rsst=usbbt=uRbt=k'*rbt
rtt=k'*uRbt2+uRbtt
k' is normal to u and r.
k'=k. => k*u=-r=nR, and
rtt=nRbt2+uRbtt
Letting variable t=s, we see bt=1/R, and curvature vector rss=nRbs2=n/R.
Therefore curvature c=1/R.
usR2bt2+uRbtt=ncR2bt2+uRbtt
At the moment, we don't see the path simpler than use formula for curvature c:
c=bs3R2=1/R.
Following is a draft:
We need vector notation for angular speed, w, which in our case simplifies to
w=r*v/RR, *-vector product.
=> v=w*r.
We will use normal to plane of motion, vector n=w0/|w0|, taken at t=0.
Then w=Wn, where W=B', is a real number which changes the sign when angle motion
changes orientation.
In complex notations: r' = irW
r''=-rWW + irW'
System O. B o d y i n C i r c u l a r M o t i o n.
Consider the system: body + rod + pin + planet.
Consider that we
1) neglect gravitation of the Planet,
2) no other forces act on body except from the rod, no air friction.
3) body size is small comparing other parameters of our system, so we
consider this body as a particle.
4) we assume that force from the rod to a body is always acts along
the line of the rod. It is obvious, but perhaps difficult to prove
when to go deeply to details with specific systems.
5) mass of the planet is much greater than mass of the body.
4) => irW''=0. Only normal acceleration exists.
=>
Full mathematical description of Equation of Motions of the particle is (EMI):
Force f=mr''=-mWWr (i)
r(0)=r0 - initial position (ii)
v(0)=v0 - initial speed (iii)
r=e(iA)R (e)
Note, that numbers F0=-mW0W0R and v0=W0R constrain each other:
v0 and R constrain W0, which constrains F0.
Otherwise, force's absolute value, F, can have any dependence from t, F(t);
however, we consider further the following system:
System I. B o d y i n U n i f o r m ? C i r c u l a r M o t i o n.
6) F=const. It is perhaps obvious that such systems exist, but difficult
to prove in each specific case.
Now, it is easy to write down a solution for above system of differential
equations (EMI):
it is simply W=const=V/R
We will use special notation for this value P (Phase speed).
This solution is unique, which should follow from corresponding mathematical
theorem which is out of scope of this intro.
For choice of initial conditions:
r0=(0,-R) (For better analogy with spring)
v0=(V,0)
the solution is:
x=Rsin(Pt)
y=-Rcos(Pt)
P=W=V/R
F=mPPR
We can add that cinetic energy is T=mVV/2=const and has two components:
for motion along each direction T=m(VxVx)/2 + m(VyVy)/2.
System II. S p r i n g. A n a l o g y w i t h S y s t e m I.
fx=-kx=Mx''
x0=0
x'(0)=V
Solution:
System (EMI) equivalent to two systems for each direction, and we
will write just for x direction:
fx=-mPPx=mx'' (*')
x(0)=0 - initial position (1')
x'(0)=V - initial speed (2')
Therefore, system for spring and x-coordinate of rotating particle are
equivalent and have the same solution if to take:
P=sqrt(k/M)
This analogy extends to following values:
Left part - circular motion, right part - spring:
Vx=x'
Ax=Vx'
m =M
Tx=T or m(VxVx)/2 = MVxVx/2
Ty=U or m(VyVy)/2 = kxx/2
E =E full energy.
System III. M a t h e m a t i c a l P e n d u l u m.
This is a System O where not only force from rod applied, but
also a gravitation force mg.
Equation of motion will look:
x''=-gsin(B)cos(B)
x0=0,
x'(0)=V.
y is bound by rod to x, we don't worry about it now:
xx+yy=RR
We assume that "rod is passive and react in such way that"
summ of forces along the rod's line is 0.
We restrict ourselves by considering the case when initial
speed V is so small that amplitude of angle B is so small that
we can use Taylor's expansion for sin and cos:
sin(B)=~B
cos(B)=~1-BB/2
To derive the condition for such approximation we equate:
mgh=mVV/2 or gh=VV/2.
h<<R <=> VV/(2g)<<R <=> WW<<g/R
x''=-gB=-(g/R)x
x0=0,
x'(0)=V.
Now, we again using solution (EMI) by taking P=sqrt(g/R):
W=Qsin(Pt), Q=W0.
We need to calculate the amplitude Q:
VV/2=QQRg. Q=sqrt(VV/(2Rg)).
W'0=QPcos(0)=V/R => QP=V/R => Q=sqrt(R/gVV/RR)=sqrt(VV/g/R)
x=Xsin(Pt), X=QR.
Vx=QRPcos(Pt).
Cinetic energy, T=mVV/2 cos(p)cos(p)
Potential energy, U=mgh=mgXW=mgsin(p)sin(p)RQQ=mVV/2 sin(p)sin(p)
We see: T+U=E.
=0 in FS-formulas.
Vectors r,v describe the motion of our particle in some approximately inertial system
which we will call "Local System" (LS). "Approximately" means that the Local System is
inertial with degree of accuracy acceptable by us. For example, for projectile
motion, we take Earth's surface as a "Local System" because Earth's movement
to common center of mass of Earth and our particle is neglectful, and both
Local System and Center of mass system can be "inertial".
Following is a draft:
A. C i r c u l a r m o t i o n.
This motion is equivalent to condition: |r|=R
=> rr=const <=>
rrt=0. (n)
Circular motion can be compactly described in complex notations:
r=Re(ib), b is an angle.
velocity =rt=iRe(ib)bt=btir=uRbt which confirms ortogonality (n) again.
acceleration=rtt=-rbt2 + uRbtt ('')
which is a summ of normal and tangent components correspondingly.
The latter result also follows from FS notations:
rt=rsst=usbbt=uRbt=k'*rbt
rtt=k'*uRbt2+uRbtt
k' is normal to u and r.
k'=k. => k*u=-r=nR, and
rtt=nRbt2+uRbtt
Letting variable t=s, we see bt=1/R, and curvature vector rss=nRbs2=n/R.
Therefore curvature c=1/R.
usR2bt2+uRbtt=ncR2bt2+uRbtt
At the moment, we don't see the path simpler than use formula for curvature c:
c=bs3R2=1/R.
Following is a draft:
We need vector notation for angular speed, w, which in our case simplifies to
w=r*v/RR, *-vector product.
=> v=w*r.
We will use normal to plane of motion, vector n=w0/|w0|, taken at t=0.
Then w=Wn, where W=B', is a real number which changes the sign when angle motion
changes orientation.
In complex notations: r' = irW
r''=-rWW + irW'
System O. B o d y i n C i r c u l a r M o t i o n.
Consider the system: body + rod + pin + planet.
Consider that we
1) neglect gravitation of the Planet,
2) no other forces act on body except from the rod, no air friction.
3) body size is small comparing other parameters of our system, so we
consider this body as a particle.
4) we assume that force from the rod to a body is always acts along
the line of the rod. It is obvious, but perhaps difficult to prove
when to go deeply to details with specific systems.
5) mass of the planet is much greater than mass of the body.
4) => irW''=0. Only normal acceleration exists.
=>
Full mathematical description of Equation of Motions of the particle is (EMI):
Force f=mr''=-mWWr (i)
r(0)=r0 - initial position (ii)
v(0)=v0 - initial speed (iii)
r=e(iA)R (e)
Note, that numbers F0=-mW0W0R and v0=W0R constrain each other:
v0 and R constrain W0, which constrains F0.
Otherwise, force's absolute value, F, can have any dependence from t, F(t);
however, we consider further the following system:
System I. B o d y i n U n i f o r m ? C i r c u l a r M o t i o n.
6) F=const. It is perhaps obvious that such systems exist, but difficult
to prove in each specific case.
Now, it is easy to write down a solution for above system of differential
equations (EMI):
it is simply W=const=V/R
We will use special notation for this value P (Phase speed).
This solution is unique, which should follow from corresponding mathematical
theorem which is out of scope of this intro.
For choice of initial conditions:
r0=(0,-R) (For better analogy with spring)
v0=(V,0)
the solution is:
x=Rsin(Pt)
y=-Rcos(Pt)
P=W=V/R
F=mPPR
We can add that cinetic energy is T=mVV/2=const and has two components:
for motion along each direction T=m(VxVx)/2 + m(VyVy)/2.
System II. S p r i n g. A n a l o g y w i t h S y s t e m I.
fx=-kx=Mx''
x0=0
x'(0)=V
Solution:
System (EMI) equivalent to two systems for each direction, and we
will write just for x direction:
fx=-mPPx=mx'' (*')
x(0)=0 - initial position (1')
x'(0)=V - initial speed (2')
Therefore, system for spring and x-coordinate of rotating particle are
equivalent and have the same solution if to take:
P=sqrt(k/M)
This analogy extends to following values:
Left part - circular motion, right part - spring:
Vx=x'
Ax=Vx'
m =M
Tx=T or m(VxVx)/2 = MVxVx/2
Ty=U or m(VyVy)/2 = kxx/2
E =E full energy.
System III. M a t h e m a t i c a l P e n d u l u m.
This is a System O where not only force from rod applied, but
also a gravitation force mg.
Equation of motion will look:
x''=-gsin(B)cos(B)
x0=0,
x'(0)=V.
y is bound by rod to x, we don't worry about it now:
xx+yy=RR
We assume that "rod is passive and react in such way that"
summ of forces along the rod's line is 0.
We restrict ourselves by considering the case when initial
speed V is so small that amplitude of angle B is so small that
we can use Taylor's expansion for sin and cos:
sin(B)=~B
cos(B)=~1-BB/2
To derive the condition for such approximation we equate:
mgh=mVV/2 or gh=VV/2.
h<<R <=> VV/(2g)<<R <=> WW<<g/R
x''=-gB=-(g/R)x
x0=0,
x'(0)=V.
Now, we again using solution (EMI) by taking P=sqrt(g/R):
W=Qsin(Pt), Q=W0.
We need to calculate the amplitude Q:
VV/2=QQRg. Q=sqrt(VV/(2Rg)).
W'0=QPcos(0)=V/R => QP=V/R => Q=sqrt(R/gVV/RR)=sqrt(VV/g/R)
x=Xsin(Pt), X=QR.
Vx=QRPcos(Pt).
Cinetic energy, T=mVV/2 cos(p)cos(p)
Potential energy, U=mgh=mgXW=mgsin(p)sin(p)RQQ=mVV/2 sin(p)sin(p)
We see: T+U=E.