Go Back to Parent Web Page
Here are the steps one usualy does when drawing in 3D.
Simplest way:
L. Projecting 3D picture to a screen. (Lens transformation.)
This is all one needs to create 3D picture.
Richer way:
R. Rotating of object.
T. Shifting (translation) object from Scene (World) coordinate center.
H. Rotating observer's head. (The same as rotating Scene around observer.)
W. Shifting (walking) observer. (The same as shifting Scene.)
SP. Rescaling front planes in 3D picture.
TP. Truncating 3D picture to fit a view pyramid.
L. Projecting 3D picture to a screen. (Lens transformation.)
TS. Truncating 2D picture to fit a screen.
SS. Rescaling 2D picture on a screen.
Steps SP and SS, TP and TS are mutually redundant.
The choice is a matter of preference.
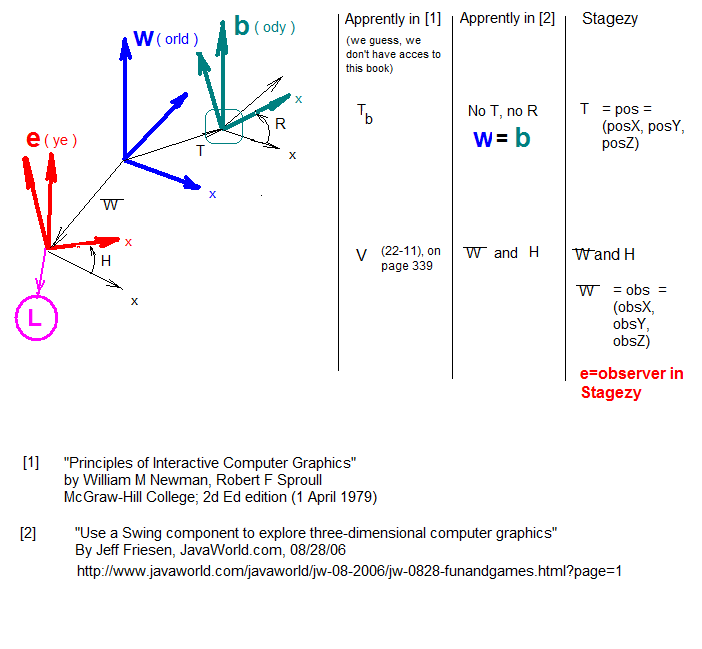 Example and modifications for Jeff Friesen's article.
Example: Steps implemented in Stagezy:
T. Hill (object, sprite) position is set constant relatively to Scene.
Moving sprites (f.e. balls) change their coordinates dynamically.
H. Arrows Left and Right.
W. Arrows Up, Down and keys PgUp and PgDown. Move observer (Vessel) along the scene.
L.
TS. Partially done. Left to Java VM to take care of.
SS. Partially done by setting constant view angle in program.
Draw in Stagezy. Continued. Draft.
We probably use simplest possible way to draw in 3D:
Step 1. We draw functions z(x,y).
Step 2. We scan square domain (x,y) from far y to close y, to shade
farer objects automatically.
Step 3. We use lens formula to project 3D function to a screen.
That's all about algorithm. There is no other sophisticated methods to do this job.
Details follow below.
Step 1.
Objects which we draw are functions z(x,y).
x,y are coordinates in horizontal plane. z is vertical coordinate.
Step 2.
Greater y corresponds to far points.
We scan a rectangular area in (x,y) plane from far y to close y.
At each y, we scan from negative x to positive x.
We set a step dx for x and dy for y which forms a horizontal net.
Four points z(x,y) at vertices of each primitive cell in the net
form cell on surface z(x,y).
Example and modifications for Jeff Friesen's article.
Example: Steps implemented in Stagezy:
T. Hill (object, sprite) position is set constant relatively to Scene.
Moving sprites (f.e. balls) change their coordinates dynamically.
H. Arrows Left and Right.
W. Arrows Up, Down and keys PgUp and PgDown. Move observer (Vessel) along the scene.
L.
TS. Partially done. Left to Java VM to take care of.
SS. Partially done by setting constant view angle in program.
Draw in Stagezy. Continued. Draft.
We probably use simplest possible way to draw in 3D:
Step 1. We draw functions z(x,y).
Step 2. We scan square domain (x,y) from far y to close y, to shade
farer objects automatically.
Step 3. We use lens formula to project 3D function to a screen.
That's all about algorithm. There is no other sophisticated methods to do this job.
Details follow below.
Step 1.
Objects which we draw are functions z(x,y).
x,y are coordinates in horizontal plane. z is vertical coordinate.
Step 2.
Greater y corresponds to far points.
We scan a rectangular area in (x,y) plane from far y to close y.
At each y, we scan from negative x to positive x.
We set a step dx for x and dy for y which forms a horizontal net.
Four points z(x,y) at vertices of each primitive cell in the net
form cell on surface z(x,y).
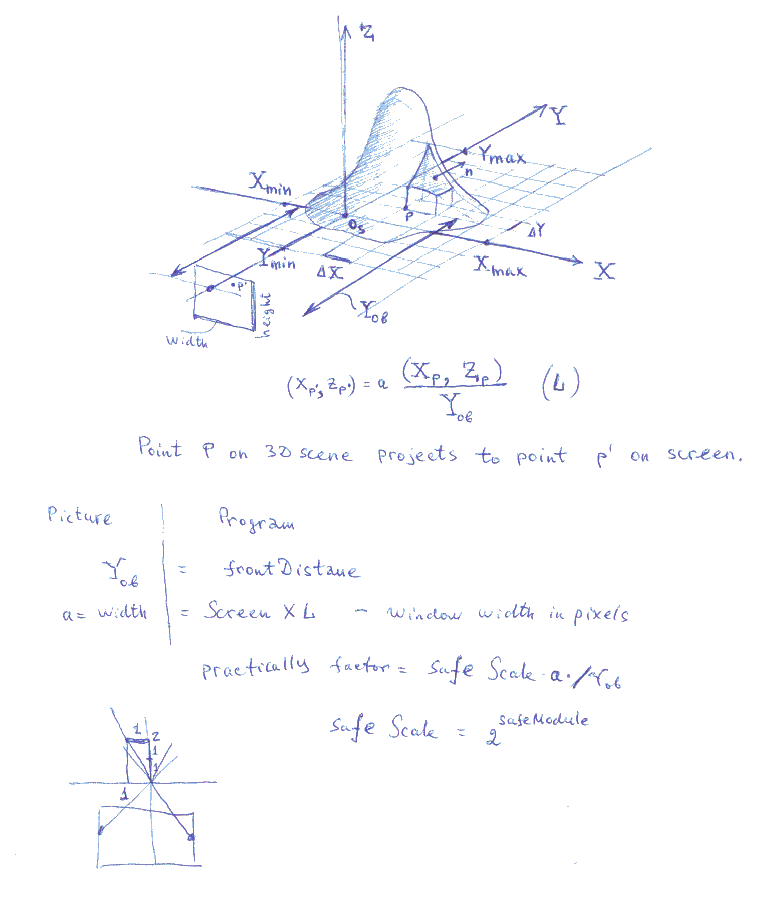 Step 2 continued:
There are two main methods which do most of 3D job:
They are in class SingleHill and are methods
ConstructHill() and PaintFunction().
ConstructHill build mesh and Paint Function paints it.
Programmer should be aware about few systems coordinates and bases we use to draw.
Step 2 continued:
There are two main methods which do most of 3D job:
They are in class SingleHill and are methods
ConstructHill() and PaintFunction().
ConstructHill build mesh and Paint Function paints it.
Programmer should be aware about few systems coordinates and bases we use to draw.
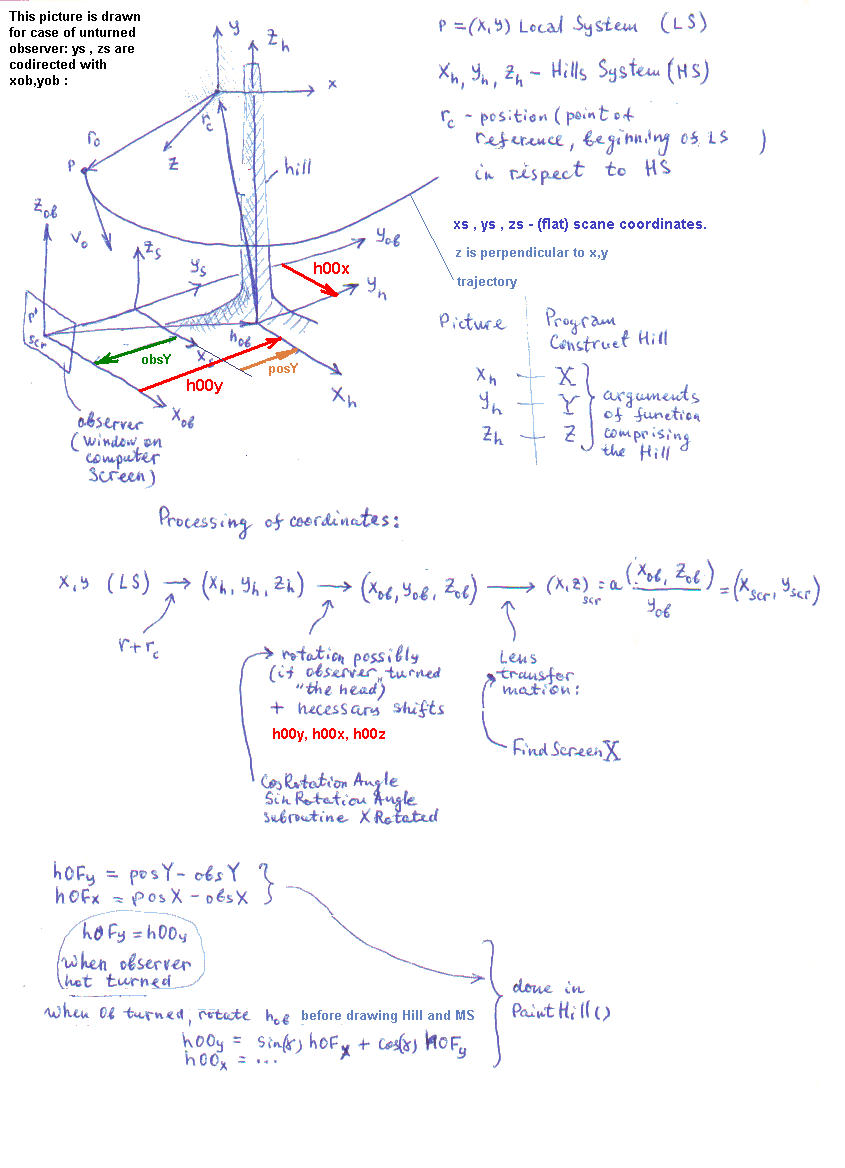 Step 3. We project this surface cell to observer's display screen using lens formula.
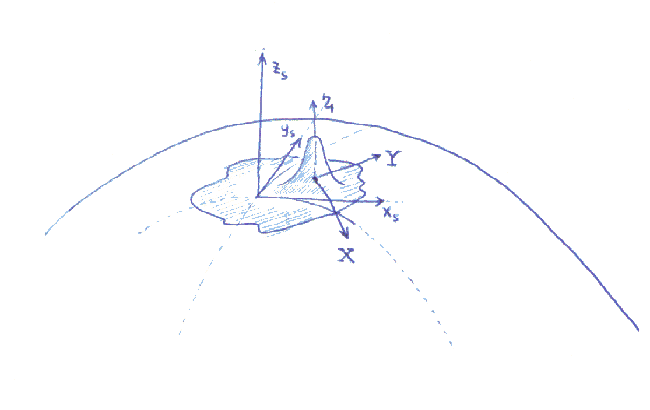
To be complete, we note that scene is embedded in to Planet like pictured here:
Step 3. We project this surface cell to observer's display screen using lens formula.
To be complete, we note that scene is embedded in to Planet like pictured here:
 More details:
a. First, we like shades on surface. Hence, we set position of light
source before we draw z(x,y).
For each surface element, we calculate unit normal vector, unit vector to
light source, and their scalar product which modifies intensity of
the color we put on surface.
b. We don't use floating point arithmetics. Only integers.
To avoid loss of accuracy, we shift coordinates x,y in area of bigger
values by multiplying them to safeScale and dividing (>>>-shifting for speed) them
when calculations are done.
c. We use custom root() method for square root based on integers.
d. We rotate Scene when user "turns the head".
e. There is a number of axiliary methods in SingleHill.java which serve for
x. overriding methods to insert drawing operations for child classes like to
insert draing trajectories, forces, moons in MechanicalSystems package.
xx. illustrational purposes like drawing vectors.
f. Terrain is also a Hill 0 which can be a background image for other hills.
More details:
a. First, we like shades on surface. Hence, we set position of light
source before we draw z(x,y).
For each surface element, we calculate unit normal vector, unit vector to
light source, and their scalar product which modifies intensity of
the color we put on surface.
b. We don't use floating point arithmetics. Only integers.
To avoid loss of accuracy, we shift coordinates x,y in area of bigger
values by multiplying them to safeScale and dividing (>>>-shifting for speed) them
when calculations are done.
c. We use custom root() method for square root based on integers.
d. We rotate Scene when user "turns the head".
e. There is a number of axiliary methods in SingleHill.java which serve for
x. overriding methods to insert drawing operations for child classes like to
insert draing trajectories, forces, moons in MechanicalSystems package.
xx. illustrational purposes like drawing vectors.
f. Terrain is also a Hill 0 which can be a background image for other hills.
 Example and modifications for Jeff Friesen's article.
Example: Steps implemented in Stagezy:
T. Hill (object, sprite) position is set constant relatively to Scene.
Moving sprites (f.e. balls) change their coordinates dynamically.
H. Arrows Left and Right.
W. Arrows Up, Down and keys PgUp and PgDown. Move observer (Vessel) along the scene.
L.
TS. Partially done. Left to Java VM to take care of.
SS. Partially done by setting constant view angle in program.
Draw in Stagezy. Continued. Draft.
We probably use simplest possible way to draw in 3D:
Step 1. We draw functions z(x,y).
Step 2. We scan square domain (x,y) from far y to close y, to shade
farer objects automatically.
Step 3. We use lens formula to project 3D function to a screen.
That's all about algorithm. There is no other sophisticated methods to do this job.
Details follow below.
Step 1.
Objects which we draw are functions z(x,y).
x,y are coordinates in horizontal plane. z is vertical coordinate.
Step 2.
Greater y corresponds to far points.
We scan a rectangular area in (x,y) plane from far y to close y.
At each y, we scan from negative x to positive x.
We set a step dx for x and dy for y which forms a horizontal net.
Four points z(x,y) at vertices of each primitive cell in the net
form cell on surface z(x,y).
Example and modifications for Jeff Friesen's article.
Example: Steps implemented in Stagezy:
T. Hill (object, sprite) position is set constant relatively to Scene.
Moving sprites (f.e. balls) change their coordinates dynamically.
H. Arrows Left and Right.
W. Arrows Up, Down and keys PgUp and PgDown. Move observer (Vessel) along the scene.
L.
TS. Partially done. Left to Java VM to take care of.
SS. Partially done by setting constant view angle in program.
Draw in Stagezy. Continued. Draft.
We probably use simplest possible way to draw in 3D:
Step 1. We draw functions z(x,y).
Step 2. We scan square domain (x,y) from far y to close y, to shade
farer objects automatically.
Step 3. We use lens formula to project 3D function to a screen.
That's all about algorithm. There is no other sophisticated methods to do this job.
Details follow below.
Step 1.
Objects which we draw are functions z(x,y).
x,y are coordinates in horizontal plane. z is vertical coordinate.
Step 2.
Greater y corresponds to far points.
We scan a rectangular area in (x,y) plane from far y to close y.
At each y, we scan from negative x to positive x.
We set a step dx for x and dy for y which forms a horizontal net.
Four points z(x,y) at vertices of each primitive cell in the net
form cell on surface z(x,y).
 Step 2 continued:
There are two main methods which do most of 3D job:
They are in class SingleHill and are methods
ConstructHill() and PaintFunction().
ConstructHill build mesh and Paint Function paints it.
Programmer should be aware about few systems coordinates and bases we use to draw.
Step 2 continued:
There are two main methods which do most of 3D job:
They are in class SingleHill and are methods
ConstructHill() and PaintFunction().
ConstructHill build mesh and Paint Function paints it.
Programmer should be aware about few systems coordinates and bases we use to draw.
 Step 3. We project this surface cell to observer's display screen using lens formula.
To be complete, we note that scene is embedded in to Planet like pictured here:
Step 3. We project this surface cell to observer's display screen using lens formula.
To be complete, we note that scene is embedded in to Planet like pictured here:
 More details:
a. First, we like shades on surface. Hence, we set position of light
source before we draw z(x,y).
For each surface element, we calculate unit normal vector, unit vector to
light source, and their scalar product which modifies intensity of
the color we put on surface.
b. We don't use floating point arithmetics. Only integers.
To avoid loss of accuracy, we shift coordinates x,y in area of bigger
values by multiplying them to safeScale and dividing (>>>-shifting for speed) them
when calculations are done.
c. We use custom root() method for square root based on integers.
d. We rotate Scene when user "turns the head".
e. There is a number of axiliary methods in SingleHill.java which serve for
x. overriding methods to insert drawing operations for child classes like to
insert draing trajectories, forces, moons in MechanicalSystems package.
xx. illustrational purposes like drawing vectors.
f. Terrain is also a Hill 0 which can be a background image for other hills.
More details:
a. First, we like shades on surface. Hence, we set position of light
source before we draw z(x,y).
For each surface element, we calculate unit normal vector, unit vector to
light source, and their scalar product which modifies intensity of
the color we put on surface.
b. We don't use floating point arithmetics. Only integers.
To avoid loss of accuracy, we shift coordinates x,y in area of bigger
values by multiplying them to safeScale and dividing (>>>-shifting for speed) them
when calculations are done.
c. We use custom root() method for square root based on integers.
d. We rotate Scene when user "turns the head".
e. There is a number of axiliary methods in SingleHill.java which serve for
x. overriding methods to insert drawing operations for child classes like to
insert draing trajectories, forces, moons in MechanicalSystems package.
xx. illustrational purposes like drawing vectors.
f. Terrain is also a Hill 0 which can be a background image for other hills.